Kai kurie skaičiavimo būdai. Determinantų skaičiavimo metodai Determinanto išplėtimas eilutėse ir stulpeliuose

Determinantai ir jų savybės. Pertvarkymas skaičiai 1, 2,..., n yra bet koks šių skaičių išdėstymas tam tikra tvarka. Elementariojoje algebroje įrodyta, kad visų permutacijų, kurias galima sudaryti iš n skaičių, skaičius yra 12...n = n!. Pavyzdžiui, iš trijų skaičių 1, 2, 3 galima sudaryti 3!=6 permutacijas: 123, 132, 312, 321, 231, 213. Sakoma, kad šioje permutacijoje skaičiai i ir j yra inversija(sutrikimas), jei i>j, bet i šioje permutacijoje yra prieš j, tai yra, jei didesnis skaičius yra kairėje nuo mažesniojo.

Permutacija vadinama net(arba nelyginis), jei jis turi lyginį (nelyginį) bendrą inversijų skaičių. Vadinama operacija, kuria pereinama nuo vienos permutacijos prie kitos, sudarytos iš tų pačių n skaičių pakeitimas n-asis laipsnis.

Pakeitimas, paverčiantis vieną permutaciją kita, rašomas dviem eilutėmis bendruose skliaustuose, o skaičiai, užimantys tas pačias vietas nagrinėjamose permutacijose, vadinami Aktualus ir yra parašyti vienas po kitu. Pavyzdžiui, simbolis reiškia pakeitimą, kuriame 3 tampa 4, 1 → 2, 2 → 1, 4 → 3. Pakeitimas vadinamas net(arba nelyginis), jei bendras inversijų skaičius abiejose pakeitimo eilutėse yra lyginis (nelyginis). Bet koks n-ojo laipsnio pakaitalas gali būti rašomas formoje, t.y. su natūraliaisiais skaičiais viršutinėje eilutėje.

Pateikiame n eilės kvadratinę matricą

. (4.3)

Panagrinėkime visas galimas n šios matricos elementų sandaugas, paimtas po vieną ir tik po vieną iš kiekvienos eilutės ir kiekvieno stulpelio, t.y. formos darbai:

, (4.4)

kur indeksai q 1, q 2,...,q n sudaro tam tikrą skaičių permutaciją
1, 2,..., n. Tokių sandaugų skaičius lygus n simbolių skirtingų permutacijų skaičiui, t.y. lygus n!. Produkto (4.4) ženklas lygus (- 1) q, kur q yra inversijų skaičius elementų antrųjų indeksų permutacijoje.

Determinantas Matricą (4.3) atitinkanti n-oji eilė vadinama algebrine suma n! formos (4.4) nariai. Norėdami parašyti determinantą, naudokite simbolį arba detA = (A matricos determinantas arba determinantas).

Determinantų savybės

1. Perkėlimo metu determinantas nekinta.

2. Jei viena iš determinanto eilučių susideda iš nulių, tai determinantas yra lygus nuliui.

3. Jei dvi determinanto eilutės bus pertvarkytos, determinantas pakeis ženklą.

4. Determinantas, turintis dvi identiškas eilutes, yra lygus nuliui.

5. Jei visi tam tikros determinanto eilutės elementai padauginami iš kokio nors skaičiaus k, tai pats determinantas bus padaugintas iš k.

6. Determinantas, kuriame yra dvi proporcingos tiesės, yra lygus nuliui.

7. Jei visi determinanto i-osios eilutės elementai pateikiami kaip dviejų terminų a i j = b j + c j (j = 1,...,n) suma, tai determinantas yra lygus determinantų sumai. kurios visos eilutės, išskyrus i-ąją, yra tokios pat kaip duotame determinante, o i-oji eilutė viename iš terminų susideda iš elementų b j , kitoje - iš elementų c j .

8. Determinantas nesikeičia, jei prie vienos iš jos eilučių elementų pridedami atitinkami kitos eilutės elementai, padauginti iš to paties skaičiaus.

komentuoti. Visos savybės lieka galioti, jei vietoj eilučių imsime stulpelius.

Nepilnametis N-osios eilės determinanto d elemento a i j vadinamas n-1 eilės determinantu, kuris gaunamas iš d išbraukus eilutę ir stulpelį, kuriuose yra šis elementas.

Algebrinis papildinys determinanto d elementas a i j vadinamas jo minoriniu M i j , paimtu su ženklu (-1) i + j . Elemento a i j algebrinis papildinys bus žymimas A i j . Taigi, A i j = (-1) i + j M i j .

Praktinio determinantų skaičiavimo metodai, pagrįsti tuo, kad n eilės determinantas gali būti išreikštas žemesnės eilės determinantais, pateikiami pagal šią teoremą.

Teorema (determinanto skaidymas eilutėje ar stulpelyje).

Determinantas yra lygus visų jo savavališkos eilutės (ar stulpelio) elementų sandaugų sumai pagal jų algebrinius papildinius. Kitaip tariant, d išplečiamas į i-osios eilutės elementus

d = a i 1 A i 1 + a i 2 A i 2 +... + a i n A i n (i = 1,...,n)

arba j stulpelis

d = a 1 j A 1 j + a 2 j A 2 j +... + a n j A n j (j =1,...,n).

Visų pirma, jei visi eilutės (arba stulpelio) elementai, išskyrus vieną, yra lygūs nuliui, tada determinantas yra lygus elementui, padaugintam iš jo algebrinio papildinio.

Trečiosios eilės determinanto skaičiavimo formulė.

Kad šią formulę būtų lengviau įsiminti:

2.4 pavyzdys. Neskaičiuodami determinanto parodykite, kad jis lygus nuliui.

Sprendimas. Iš antrosios eilutės atėmus pirmąjį, gauname determinantą, lygų pradiniam. Jei iš trečiosios eilutės taip pat atimame pirmąją, gauname determinantą, kuriame dvi eilutės yra proporcingos. Šis determinantas yra lygus nuliui.

Sprendimas. Jei prie kiekvienos determinanto eilutės pridėsite pirmąją eilutę, pradedant nuo antrosios, gausite determinantą, kuriame visi elementai žemiau pagrindinės įstrižainės bus lygūs nuliui. Būtent, mes gauname determinantą: , lygus pradiniam.

Samprotaudami kaip ir ankstesniame pavyzdyje, nustatome, kad jis lygus pagrindinės įstrižainės elementų sandaugai, t.y. n!. Metodas, kuriuo šis determinantas apskaičiuojamas, vadinamas redukavimo į trikampę formą metodu.

SAVYBĖ 1. Determinanto reikšmė nepasikeis, jei visos jo eilutės bus pakeistos stulpeliais, o kiekviena eilutė bus pakeista stulpeliu su tuo pačiu numeriu, tai yra

SAVYBĖ 2. Dviejų determinanto stulpelių arba dviejų eilučių pertvarkymas prilygsta jo padauginimui iš -1. Pavyzdžiui,

SAVYBĖ 3. Jei determinantas turi du vienodus stulpelius arba dvi identiškas eilutes, tada jis yra lygus nuliui.

SAVYBĖ 4. Vieno determinanto vieno stulpelio arba vienos eilutės elementų padauginimas iš bet kurio skaičiaus k yra tolygus determinanto padauginimui iš šio skaičiaus k. Pavyzdžiui,

SAVYBĖ 5. Jeigu kurio nors stulpelio ar kurios nors eilutės visi elementai lygūs nuliui, tai pats determinantas lygus nuliui. Ši savybė yra ypatingas ankstesnio atvejis (jei k = 0).

SAVYBĖ 6. Jei determinanto dviejų stulpelių arba dviejų eilučių atitinkami elementai yra proporcingi, tai determinantas lygus nuliui.

SAVYBĖ 7. Jei kiekvienas determinanto n-ojo stulpelio arba n-osios eilutės elementas yra dviejų narių suma, tai determinantas gali būti pavaizduotas kaip dviejų determinantų suma, iš kurių vienas yra n-ame stulpelyje arba, atitinkamai, n-oje. eilutėje yra pirmasis iš minėtų terminų, o kitoje – antrasis; likusiose vietose esantys elementai yra vienodi trijų determinantų etapams. Pavyzdžiui,

SAVYBĖ 8. Jei prie tam tikro stulpelio (ar kokios nors eilutės) elementų pridėsime atitinkamus kito stulpelio (ar kitos eilutės) elementus, padaugintus iš bet kurio bendro koeficiento, tai determinanto reikšmė nepasikeis. Pavyzdžiui,

Kitos determinantų savybės yra susijusios su algebrinio komplemento ir minoro sąvoka. Elemento minoras yra determinantas, gautas iš tam tikro elemento perbraukus eilutę ir stulpelį, kurių sankirtoje šis elementas yra.

Bet kurio determinanto elemento algebrinis papildinys yra lygus šio elemento mažajai, paimtai su jo ženklu, jei eilutės ir stulpelio, kurių sankirtoje yra elementas, skaičių suma yra lyginis skaičius, ir su priešingas ženklas, jei šis skaičius nelyginis.

Elemento algebrinį papildymą žymėsime didžiąja to paties pavadinimo raide ir tuo pačiu skaičiumi kaip ir patį elementą žyminčią raidę.

TURTAS 9. Determinantas

yra lygus bet kurio stulpelio (arba eilutės) elementų sandaugų sumai pagal jų algebrinius papildinius.

Kitaip tariant, galioja šios lygybės:

, ,

, .

6) Minorai ir algebriniai priedai.

Apibrėžimas. Mažasis determinanto elementas yra th įsakymas paskambino determinantas– užsakymas, kuris gaunamas iš duotosios determinantas perbraukiant -tą eilutę ir -stulpelį, kurių sankirtoje yra elementas.

Pavadinimas:.

Apibrėžimas. 1-osios eilės determinanto elemento algebrinis papildinys yra jo minorinis, imamas su pliuso ženklu, jei jis lyginis, ir su minuso ženklu priešingu atveju.

Pavadinimas:.

Teorema. (Dėl determinanto išplėtimo.)

Determinantas yra lygus bet kurios determinanto eilutės (ar bet kurio stulpelio) elementų ir jų algebrinių papildinių sandaugų sumai:

7) Atvirkštinė matrica- toks matrica A −1 , padauginus iš kurio, pradinė matrica A rezultatus tapatybės matrica E:

Kvadratinė matrica yra grįžtamasis tada ir tik tada, kai yra neišsigimęs, tai yra jo determinantas nelygu nuliui. Ne kvadratinėms matricoms ir vienaskaitos matricos atvirkštinių matricų nėra. Tačiau galima šią sąvoką apibendrinti ir įvesti pseudoinversinės matricos, panašus į atvirkštinį daugelio savybių.

8)Matricos rangas- didžiausias užsakymų skaičius nepilnamečiųšios matricos, ne nulis

Paprastai matricos rangas žymimas () arba . Abu pavadinimai atėjo pas mus iš užsienio kalbų, todėl gali būti vartojami abu.

Savybės

Teorema (apie bazinį minorą): Tegu r = rang A M yra matricos A bazinis minoras, tada:

pagrindinės eilutės ir stulpeliai yra tiesiškai nepriklausomi;

bet kuri matricos A eilutė (stulpelis) yra tiesinis bazinių eilučių (stulpelių) derinys.

Galima priderinti prie kai kurių numerį, apskaičiuotas pagal tam tikrą taisyklę ir vadinamas determinantas.

Būtinybė pristatyti koncepciją determinantas - numeriai, charakterizuojantis kvadratas užsakymo matrica n , yra glaudžiai susijęs su tiesinių algebrinių lygčių sistemų sprendimu.

Matricos determinantas A pažymėsime: | A| arba D.

Pirmosios eilės matricos determinantasA = (A 11) elementas vadinamas A vienuolika . Pavyzdžiui, už A= (-4) turime | A| = -4.

Antros eilės matricos determinantas paskambino numerį, nustatoma pagal formulę

|A| = .

Pavyzdžiui, | A| = .

Žodžiais šią taisyklę galima parašyti taip: su savo ženklu reikia paimti sujungtų elementų sandaugą pagrindinė įstrižainė, o elementų, sujungtų trikampių viršūnėmis, sandauga pagrindas lygiagrečiai pagrindinei įstrižai. Su priešingu ženklu imami panašūs produktai, tik antrinės įstrižainės atžvilgiu.

Pavyzdžiui,

Matricos determinanto apibrėžimas n Užsakymo neduosime, o tik parodysime būdą kaip jį rasti.

Vėliau vietoj žodžių matricos determinantas n– įsakymas tiesiog pasikalbėkime determinantas n– įsakymas. Pristatykime naujas sąvokas.

Tegu pateikta kvadratinė matrica n– įsakymas.

NepilnametisM elementas ij A ij matricos A paskambino determinantas (n-1) eilė, gauta iš matricos A perbraukiant i-toji eilutė ir j stulpelis.

Matricos A elemento a ij algebrinis papildinys A ij yra jo minoras, paimtas su ženklu (-1) i+j:

A ij = (-1) i + j M ij,

tie. algebrinis papildinys arba sutampa su mažuoju, kai eilučių ir stulpelių skaičių suma yra lyginis skaičius, arba skiriasi nuo jo ženklu, kai eilutės ir stulpelio skaičių suma yra nelyginis skaičius.

Pavyzdžiui, elementams A 11 ir A 12 matricų A = nepilnamečių

M 11 = A 11 = ,

M 12 = ,

A A 12 = (-1) 1+2 M 12 = -8.

Teorema (apie determinanto išplėtimą) . Kvadratinės matricos determinantas yra lygus bet kurios eilutės (stulpelio) elementų sandaugų sumai pagal jų algebrinius papildinius, t.y.

|A| = A i1 A i1+ A i2 A i2 + … + A in Aį,
bet kam i = 1, 2, …, n

|A| = A 1j A 1j + A 2j A 2j + … + A nj A nj,

bet kam j = 1, 2, …, n

Pirmoji formulė vadinama i-toji eilutė, o antrasis - determinanto išplėtimas į elementus j stulpelis.

Nesunku suprasti, kad naudojant šias formules bet koks determinantas n Eilė gali būti sumažinta iki determinantų sumos, kurios eilė bus 1 mažesnė ir pan. kol pasieksime 3 ar 2 eilės determinantus, kurių skaičiavimas nebėra sunkus.

Norint rasti determinantą, gali būti taikomos šios pagrindinės savybės:

1. Jei kuri nors determinanto eilutė (ar stulpelis) susideda iš nulių, tai pats determinantas yra lygus nuliui.

2. Pertvarkant bet kurias dvi eilutes (arba du stulpelius), determinantas dauginamas iš -1.

3. Determinantas su dviem lygiomis arba proporcingomis eilutėmis (ar stulpeliais) yra lygus nuliui.

4. Bet kurios eilutės (ar stulpelio) elementų bendras koeficientas gali būti išimtas iš determinanto ženklo.

5. Determinanto reikšmė nepasikeis, jei bus pakeistos visos eilutės ir stulpeliai.

6. Determinanto reikšmė nepasikeis, jei prie vienos iš eilučių (arba į vieną iš stulpelių) bus pridėta kita eilutė (stulpelis), padauginta iš bet kurio skaičiaus.

7. Bet kurios matricos eilutės (ar stulpelio) elementų sandaugų suma kitos šios matricos eilutės (stulpelio) elementų algebriniais papildiniais yra lygi nuliui.

8. Dviejų kvadratinių matricų sandaugos determinantas yra lygus jų determinantų sandaugai.

Matricos determinanto sąvokos įvedimas leidžia apibrėžti kitą operaciją su matricomis – matricos atvirkštinės vertės radimą.

Kiekvienam skaičiui, kuris nėra nulis, yra atvirkštinis skaičius, todėl šių skaičių sandauga suteikia vieną. Kvadratinių matricų atveju taip pat yra tokia koncepcija.

Matrica A-1 vadinamas atvirkščiai link kvadratas matrica A, jei padauginus šią matricą iš duotosios ir dešinėje, ir kairėje paaiškėja tapatybės matrica, t.y.

A× A -1 = A-1× A= E.

Iš apibrėžimo matyti, kad tik kvadratinė matrica turi atvirkštinę vertę; šiuo atveju atvirkštinė matrica bus tos pačios eilės kvadratas. Tačiau ne kiekviena kvadratinė matrica turi atvirkštinę.

ALGEBRINIAI PAPILDYMAI IR NEPALAIKIAI

Turėkime trečios eilės determinantą: .

Nepilnametis, atitinkantis šį elementą a ij trečios eilės determinantu vadinamas antros eilės determinantas, gautas iš duotosios, išbraukus eilutę ir stulpelį, kurių sankirtoje duotasis elementas stovi, t.y. i-toji eilutė ir j stulpelis. Nepilnamečiai, atitinkantys duotą elementą a ij pažymėsime M ij.

Pavyzdžiui, nepilnametis M 12, atitinkantis elementą a 12, bus lemiamas veiksnys , kuris gaunamas iš šio determinanto išbraukus 1 eilutę ir 2 stulpelį.

Taigi, formulė, apibrėžianti trečiosios eilės determinantą, rodo, kad šis determinantas yra lygus 1-osios eilės elementų sandaugų sumai pagal atitinkamus nepilnamečius; šiuo atveju elementą atitinkantis nepilnametis a 12, imamas su „–“ ženklu, t.y. galime tai parašyti

(1)

Panašiai galima įvesti nepilnamečių apibrėžimus antros ir aukštesnės eilės determinantams.

Pristatykime dar vieną koncepciją.

Algebrinis papildinys elementas a ij determinantas vadinamas jo nepilnamečiu M ij, padauginta iš (–1) i+j .

Algebrinis elemento papildinys a ijžymimas A ij.

Iš apibrėžimo gauname, kad ryšys tarp elemento algebrinio papildinio ir jo minorinio išreiškiamas lygybe A ij= (–1) i+j Mij.

Pavyzdžiui,

Pavyzdys. Pateikiamas determinantas. Rasti A 13, A 21, A 32.

Nesunku pastebėti, kad naudojant algebrinius elementų papildymus, formulę (1) galima parašyti taip:

Panašiai kaip ir šioje formulėje, galite gauti determinanto išplėtimą į bet kurios eilutės ar stulpelio elementus.

Pavyzdžiui, determinanto išskaidymas į 2-os eilutės elementus gali būti gautas taip. Pagal determinanto 2 savybę turime:

Išplėskime gautą determinantą į 1-os eilutės elementus.

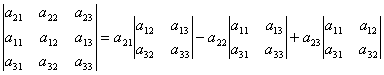(2)

Iš čia nes antros eilės determinantai formulėje (2) yra mažieji elementų elementai 21, 22, 23. Taigi, t.y. gavome determinanto išskaidymą į 2-os eilės elementus.

Panašiai galime gauti determinanto išplėtimą į trečiosios eilutės elementus. Naudodami determinantų 1 savybę (apie perkėlimą), galime parodyti, kad panašūs išplėtimai galioja ir plečiant stulpelių elementus.

Taigi galioja sekanti teorema.

Teorema (apie determinanto išplėtimą per tam tikrą eilutę ar stulpelį). Determinantas yra lygus bet kurios iš jo eilučių (ar stulpelių) elementų ir jų algebrinių papildinių sandaugų sumai.

Visa tai, kas išdėstyta pirmiau, galioja ir bet kurios aukštesnės eilės determinantams.

Pavyzdžiai.

ATvirkštinė matrica

Atvirkštinės matricos sąvoka įvedama tik kvadratinės matricos.

Jeigu A tada yra kvadratinė matrica atvirkščiai jam matrica yra matrica, pažymėta A-1 ir tenkina sąlygą. (Šis apibrėžimas įvedamas pagal analogiją su skaičių daugyba)

Bendruoju atveju $n$-osios eilės determinantų skaičiavimo taisyklė yra gana sudėtinga. Antros ir trečios eilės determinantams yra racionalių būdų juos apskaičiuoti.

Antros eilės determinantų skaičiavimai

Norėdami apskaičiuoti antrosios eilės matricos determinantą, turite atimti antrinės įstrižainės elementų sandaugą iš pagrindinės įstrižainės elementų sandaugos:

$$\left| \begin(masyvas)(ll)(a_(11)) & (a_(12)) \\ (a_(21)) & (a_(22))\end(masyvas)\right|=a_(11) \ cdot a_(22)-a_(12) \cdot a_(21)$$

Pavyzdys

Pratimas. Apskaičiuokite antros eilės determinantą $\left| \begin(masyvas)(rr)(11) & (-2) \\ (7) & (5)\end(masyvas)\right|$

Sprendimas.$\left| \begin(masyvas)(rr)(11) & (-2) \\ (7) & (5)\end(masyvas)\right|=11 \cdot 5-(-2) \cdot 7=55+14 = 69 USD

Atsakymas.$\left| \begin(masyvas)(rr)(11) & (-2) \\ (7) & (5)\end(masyvas)\right|=69 $

Trečios eilės determinantų skaičiavimo metodai

Trečiosios eilės determinantams apskaičiuoti taikomos šios taisyklės.

Trikampio taisyklė

Schematiškai ši taisyklė gali būti pavaizduota taip:

Pirmojo determinanto elementų, sujungtų tiesiomis linijomis, sandauga paimama su pliuso ženklu; panašiai ir antrajam determinantui atitinkami sandaugai imami su minuso ženklu, t.y.

$$\left| \begin(masyvas)(ccc)(a_(11)) & (a_(12)) & (a_(13)) \\ (a_(21)) & (a_(22)) & (a_(23)) \\ (a_(31)) & (a_(32)) & (a_(33))\end(masyvas)\right|=a_(11) a_(22) a_(33)+a_(12) a_( 23) a_(31)+a_(13) a_(21) a_(32)-$$

$$-a_(11) a_(23) a_(32)-a_(12) a_(21) a_(33)-a_(13) a_(22) a_(31)$$

Pavyzdys

Pratimas. Apskaičiuokite $\left| determinantą \begin(masyvas)(rrr)(3) & (3) & (-1) \\ (4) & (1) & (3) \\ (1) & (-2) & (-2)\pabaiga (masyvas)\right|$ naudojant trikampio metodą.

Sprendimas.$\left| \begin(masyvas)(rrr)(3) & (3) & (-1) \\ (4) & (1) & (3) \\ (1) & (-2) & (-2)\pabaiga (masyvas)\right|=3 \cdot 1 \cdot(-2)+4 \cdot(-2) \cdot(-1)+$

$$+3 \cdot 3 \cdot 1-(-1) \cdot 1 \cdot 1-3 \cdot(-2) \cdot 3-4 \cdot 3 \cdot(-2)=54$$

Atsakymas.

Sarrus valdo

Determinanto dešinėje pridėkite pirmuosius du stulpelius ir paimkite elementų sandaugas pagrindinėje įstrižainėje ir jai lygiagrečiose įstrižainėse su pliuso ženklu; o antrinės įstrižainės ir jai lygiagrečių įstrižainių elementų sandaugos su minuso ženklu:

$$-a_(13) a_(22) a_(31)-a_(11) a_(23) a_(32)-a_(12) a_(21) a_(33)$$

Pavyzdys

Pratimas. Apskaičiuokite $\left| determinantą \begin(masyvas)(rrr)(3) & (3) & (-1) \\ (4) & (1) & (3) \\ (1) & (-2) & (-2)\pabaiga (masyvas)\right|$ naudojant Sarrus taisyklę.

Sprendimas.

$$+(-1) \cdot 4 \cdot(-2)-(-1) \cdot 1 \cdot 1-3 \cdot 3 \cdot(-2)-3 \cdot 4 \cdot(-2)= 54 USD

Atsakymas.$\left| \begin(masyvas)(rrr)(3) & (3) & (-1) \\ (4) & (1) & (3) \\ (1) & (-2) & (-2)\pabaiga (masyvas)\right|=54$

Determinanto išplėtimas pagal eilutę arba stulpelį

Determinantas lygus determinanto eilutės elementų ir jų algebrinių papildinių sandaugų sumai. Paprastai pasirenkama eilutė / stulpelis, kuriame yra nuliai. Eilutė ar stulpelis, išilgai kurio atliekamas skaidymas, bus pažymėtas rodykle.

Pavyzdys

Pratimas. Išplėsdami pirmąją eilutę, apskaičiuokite determinantą $\left| \begin(masyvas)(lll)(1) & (2) & (3) \\ (4) & (5) & (6) \\ (7) & (8) & (9)\end(masyvas) \right|$

Sprendimas.$\left| \begin(masyvas)(lll)(1) & (2) & (3) \\ (4) & (5) & (6) \\ (7) & (8) & (9)\end(masyvas) \dešinė| \leftarrow=a_(11) \cdot A_(11)+a_(12) \cdot A_(12)+a_(13) \cdot A_(13)=$

Atsakymas.

Šis metodas leidžia determinanto apskaičiavimą redukuoti iki žemesnės eilės determinanto skaičiavimo.

Pavyzdys

Pratimas. Apskaičiuokite $\left| determinantą \begin(masyvas)(lll)(1) & (2) & (3) \\ (4) & (5) & (6) \\ (7) & (8) & (9)\end(masyvas) \right|$

Sprendimas. Determinanto eilėse atliksime tokias transformacijas: iš antros eilės atimame pirmąsias keturias, o iš trečios pirmąją eilutę padauginsime iš septynių, dėl to pagal determinanto savybes gauname determinantą lygus duotam.

$$\left| \begin(masyvas)(ccc)(1) & (2) & (3) \\ (4) & (5) & (6) \\ (7) & (8) & (9)\end(masyvas) \right|=\left| \begin(masyvas)(ccc)(1) & (2) & (3) \\ (4-4 \cdot 1) & (5-4 \cdot 2) & (6-4 \cdot 3) \\ ( 7-7 \cdot 1) & (8-7 \cdot 2) & (9-7 \cdot 3)\end(masyvas)\right|=$$

$$=\left| \begin(masyvas)(rrr)(1) & (2) & (3) \\ (0) & (-3) & (-6) \\ (0) & (-6) & (-12)\ end(masyvas)\right|=\left| \begin(masyvas)(ccc)(1) & (2) & (3) \\ (0) & (-3) & (-6) \\ (0) & (2 \cdot(-3)) & (2 \cdot(-6))\end(masyvas)\right|=0$$

Determinantas yra nulis, nes antroji ir trečioji eilutės yra proporcingos.

Atsakymas.$\left| \begin(masyvas)(lll)(1) & (2) & (3) \\ (4) & (5) & (6) \\ (7) & (8) & (9)\end(masyvas) \right|=0$

Ketvirtosios ir aukštesnės eilės determinantams apskaičiuoti naudojamas eilutės / stulpelio išplėtimas arba sumažinimas iki trikampio formos, arba Laplaso teorema.

Determinanto skaidymas į eilutės ar stulpelio elementus

Pavyzdys

Pratimas. Apskaičiuokite $\left| determinantą \begin(masyvas)(llll)(9) & (8) & (7) & (6) \\ (5) & (4) & (3) & (2) \\ (1) & (0) & (1) & (2) \\ (3) & (4) & (5) & (6)\end(masyvas)\right|$ , išskaidydami jį į kokios nors eilutės ar stulpelio elementus.

Sprendimas. Pirmiausia atlikime elementarias transformacijas determinanto eilutėse, padarydami kuo daugiau nulių arba eilutėje, arba stulpelyje. Norėdami tai padaryti, pirmiausia atimkite devynis trečdalius iš pirmosios eilutės, penkis trečdalius iš antrosios ir tris trečdalius iš ketvirtosios, gauname:

$$\left| \begin(masyvas)(cccc)(9) & (8) & (7) & (6) \\ (5) & (4) & (3) & (2) \\ (1) & (0) & (1) & (2) \\ (3) & (4) & (5) & (6)\end(masyvas)\right|=\left| \begin(masyvas)(cccc)(9-1) & (8-0) & (7-9) & (6-18) \\ (5-5) & (4-0) & (3-5) & (2-10) \\ (1) & (0) & (1) & (2) \\ (0) & (4) & (2) & (0)\end(masyvas)\right|=\ paliko| \begin(masyvas)(rrrr)(0) & (8) & (-2) & (-12) \\ (0) & (4) & (-2) & (-8) \\ (1) & (0) & (1) & (2) \\ (0) & (4) & (2) & (0)\end(masyvas)\right|$$

Išskaidykime gautą determinantą į pirmojo stulpelio elementus:

$$\left| \begin(masyvas)(rrrr)(0) & (8) & (-2) & (-12) \\ (0) & (4) & (-2) & (-8) \\ (1) & (0) & (1) & (2) \\ (0) & (4) & (2) & (0)\end(masyvas)\right|=0+0+1 \cdot(-1)^( 3+1) \cdot \left| \begin(masyvas)(rrr)(8) & (-2) & (-12) \\ (4) & (-2) & (-8) \\ (4) & (2) & (0)\ end(masyvas)\right|+0$$

Taip pat gautą trečiosios eilės determinantą išplėsime į eilutės ir stulpelio elementus, anksčiau gavę nulius, pavyzdžiui, pirmame stulpelyje. Norėdami tai padaryti, iš pirmosios eilutės atimkite antras dvi eilutes, o iš trečiosios - antrą:

$$\left| \begin(masyvas)(rrr)(8) & (-2) & (-12) \\ (4) & (-2) & (-8) \\ (4) & (2) & (0)\ end(masyvas)\right|=\left| \begin(masyvas)(rrr)(0) & (2) & (4) \\ (4) & (-2) & (-8) \\ (0) & (4) & (8)\end( masyvas)\right|=4 \cdot(-1)^(2+2) \cdot \left| \begin(masyvas)(ll)(2) & (4) \\ (4) & (8)\end(masyvas)\right|=$$

$$=4 \cdot(2 \cdot 8-4 \cdot 4)=0$$

Atsakymas.$\left| \begin(masyvas)(cccc)(9) & (8) & (7) & (6) \\ (5) & (4) & (3) & (2) \\ (1) & (0) & (1) & (2) \\ (3) & (4) & (5) & (6)\end(masyvas)\right|=0$

komentuoti

Paskutinio ir priešpaskutinio determinantų apskaičiuoti nepavyko, bet iš karto daroma išvada, kad jie lygūs nuliui, nes juose yra proporcingų eilučių.

Determinanto sumažinimas iki trikampio formos

Naudojant elementariąsias transformacijas per eilutes ar stulpelius, determinantas redukuojamas į trikampę formą, o tada jo reikšmė pagal determinanto savybes yra lygi pagrindinės įstrižainės elementų sandaugai.

Pavyzdys

Pratimas. Apskaičiuokite determinantą $\Delta=\left| \begin(masyvas)(rrrr)(-2) & (1) & (3) & (2) \\ (3) & (0) & (-1) & (2) \\ (-5) & ( 2) & (3) & (0) \\ (4) & (-1) & (2) & (-3)\end(masyvas)\right|$ sumažinant jį iki trikampio formos.

Sprendimas. Pirmiausia pirmame stulpelyje po pagrindine įstriža padarome nulius. Visas transformacijas bus lengviau atlikti, jei elementas $a_(11)$ bus lygus 1. Norėdami tai padaryti, sukeisime pirmąją ir antrąją determinanto stulpelius, kurie pagal determinanto savybes jį sukels. pakeisti ženklą į priešingą:

$$\Delta=\left| \begin(masyvas)(rrrr)(-2) & (1) & (3) & (2) \\ (3) & (0) & (-1) & (2) \\ (-5) & ( 2) & (3) & (0) \\ (4) & (-1) & (2) & (-3)\end(masyvas)\right|=-\left| \begin(masyvas)(rrrr)(1) & (-2) & (3) & (2) \\ (0) & (3) & (-1) & (2) \\ (2) & (- 5) & (3) & (0) \\ (-1) & (4) & (2) & (-3)\end(masyvas)\right|$$

$$\Delta=-\left| \begin(masyvas)(rrrr)(1) & (-2) & (3) & (2) \\ (0) & (3) & (-1) & (2) \\ (0) & (- 1) & (-3) & (-4) \\ (0) & (2) & (5) & (-1)\end(masyvas)\right|$$

Toliau vietoje elementų, esančių po pagrindine įstriža, antrame stulpelyje gauname nulius. Vėlgi, jei įstrižainės elementas yra lygus $\pm 1$, tada skaičiavimai bus paprastesni. Norėdami tai padaryti, pakeiskite antrąją ir trečiąją eilutes (ir tuo pačiu pakeiskite į priešingą determinanto ženklą):

$$\Delta=\left| \begin(masyvas)(rrrr)(1) & (-2) & (3) & (2) \\ (0) & (-1) & (-3) & (-4) \\ (0) & (3) & (-1) & (2) \\ (0) & (2) & (5) & (-1)\end(masyvas)\right|$$

Gali būti naudinga perskaityti: